퍼셉트론 개념
퍼셉트론은 인공신경망의 구성요소로서 다수의 값을 입력받아 하나의 값으로 출력하는 알고리즘.
입력값 X 가중치, 편향(bias)은 퍼셉트론으로 전달됩니다.
퍼셉트론은 입력받은 값을 모두 합산하는데, 합산된 결과값을 가중합이라 부릅니다.
앞서 생물학적 뉴런은 신경세포체에 저장한 신호의 크기가 임계값(세타)보다 클 때 신호를 출력한다고 했습니다.
퍼셉트론에서도 가중합의 크기를 임계값(세타)과 비교하는
활성화 함수(Activation Function)를 거쳐 최종 출력값을 결정.
weight의 크기는 bias의 크기로 조절할 수 있으므로, bias가 퍼셉트론의 출력값 y를 결정짓는 중요 변수인 셈
퍼셉트론 종류
퍼셉트론의 종류는 input layer ,output layer 사이에 hidden layer 의 존재 여부에 따라
단층 퍼셉트론(single layer)과 다층 퍼셉트론(multi layer)으로 나뉩니다.
퍼셉트론 학습 방법

여기서 입력값 x 자체는 변경하지 않고 2가지 클래스를 잘 분류하는 기준선을 찾는 방법은 크게 2가지가 있음
1) bias 조정(b)
첫 번째 방법은 상수값 bias(b)를 조정하는 것, 바이어스는 직선의 절편을 의미하여 , 편향 값을 조정함으로서 직선 자체를 이동시킬 수 있음
2)가중치(w) 조정
두번째 방법은 가중치(w)를 조정하는 것, 가중치는 쉽게 말해서 직선의 기울기 , 조정한 가중치는 아래와 같은 수식에 따라 산출

3) 퍼셉트론 학습 절차
퍼셉트론은 아래와 같은 절차로 최적의 직선을 찾아나갑니다.
1)좌표평면에 임의의 직선을 그음
2) 데이터를 하나씩 입력
3) 입력값에 따른 모델의 예측값과 정답을 비교하여 틀린 경우 직선을 다시 그음
4) 모든 학습용 데이터에 (2),(3) 을 반복
MSE 개념
평균 제곱 오차는 이름에서 알 수 있듯이 오차를 제곱한 값의 평균, 오차판 알고리즘이 예측한 값과 실제 정답과의 차이를 의미.
즉, 알고리즘이 정답을 잘 맞출수록 MSE값은 작아짐, MSE 값이 작을수록 알고리즘의 성능이 좋음, outlier에 민감


수식에서 1/2는 convention으로 일반적으로 사용되는 값 , 사용 이유는 MSE를 미분했을 때 제곱역할을 하는 지수가 전체 식에 상수 2로서 곱해지기 때문에 이를 제거하기 위함 (1/2 가 없어도 됨)
특징
MSE는 오차가 커질 수록 손실 함수 값이 빠르게 증가하는 특징이 있음, 그림 2는 MSE를 좌표평면에 나타낸 것
손실 함수(E)의 크기는 오차의 제곱에 비례하여 변하는 것을 볼 수 있음. 그만큼 미분값이 일정하지 않고 오차가 커질 수록 미분 값 역시 커지는 것을 알 수 있음. MSE와는 다르게 평균 절대오차(MAE)는 오차가 커질 수록 손실 함수가 선형적으로 증가, MAE와 비교했을 때 MSE가 비교적 오차의 변화량에 따라 손실 함수 값이 크게 변한다는 것을 알 수 있음
MAE 개념
평균절대오차(Mean Absolute Error, MAE)는 모든 절대 오차(Error)의 평균입니다. 여기서 오차란 알고리즘이 예측한 값과 실제 정답과의 차이를 의미합니다. 즉, 알고리즘이 정답을 잘 맞힐수록 MSE 값은 작습니다. 따라서, MAE가 작을수록 알고리즘의 성능이 좋다고 볼 수 있습니다. MAE의 수식을 살펴보겠습니다.

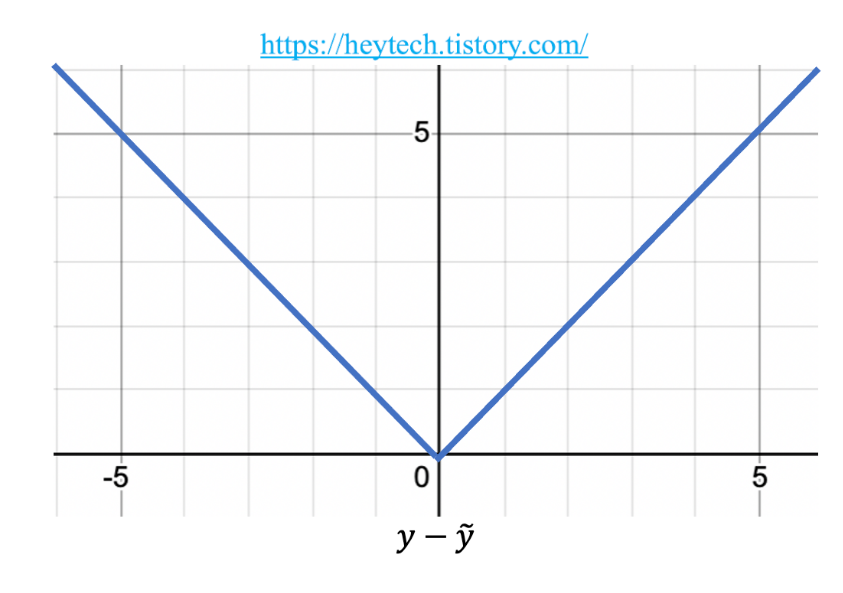
MAE는 손실 함수가 오차와 비례하여 일정하게 증가하는 특징이 있습니다(그림 1 참고). MAE와 달리, 평균제곱오차(MSE)는 오차 제곱의 평균값이므로 오차가 커질수록 손실 함수의 값이 빠르게 증가한다는 특징이 있습니다. 평균제곱오차 관련 포스팅은 이곳을 참고해 주세요. 이와 같은 특징 덕분에, MAE는 Outlier에 강건하다는(Robust) 특징이 있습니다. 다음 섹션에서 이에 대해 자세히 알아봅니다.
Outlier에 강건하다는 것은 오차가 유난히 큰 값은 Outlier로서 간주하여 해당 값을 무시하고 학습한다는 의미입니다. 예를 들어, 모델 학습이 잘 되었다면 위의 그림 2와 같이 대부분의 오차가 작기 때문에 밀집되어 나타날 것입니다. 그 와중에 그림 2의 우측 상단 빨간 점과 같이 오차가 유난히 큰 Outlier가 있을 수 있습니다. MAE는 모든 오차의 평균 합입니다. 즉, MAE의 경우, Outlier의 오차를 줄이기 위해 잘 추정된 녹색 데이터의 값을 모두 변화시켜 얻는 Loss 이득이나 Outlier의 큰 오차를 무시하고 현재 상태에서 학습을 진행할 때의 Loss 이득이 동일합니다. 따라서 MAE는 이러한 Outlier를 무시하고 학습을 진행합니다. 즉, MAE는 Outlier가 있어도 최대한 잘 추정된 데이터들의 특성을 반영할 수 있기 때문에 통계적으로 중앙값(Median)과 연관이 깊습니다. 반면 MSE의 경우, 에러 값이 증가함에 따라 손실 함수가 제곱배 만큼 커지기 때문에, Outlier의 오차를 줄이면 얻을 수 있는 Loss 이득이 훨씬 큽니다. 즉, MSE는 Outlier에 민감하다는 특징이 있습니다.
2.3. 회귀 문제에 활용
'Deep Learning' 카테고리의 다른 글
| Sigmoid vs Softmax (1) | 2023.11.01 |
|---|---|
| 최적화 개념과 gradient descent (0) | 2023.09.23 |
| 손실함수 , 활성함수 정리 (0) | 2023.09.06 |
| Embedding layer와 Embedding Vector의 Output 차이 정리 (0) | 2023.02.14 |
| Embedding Vector 과정 및 정의 (0) | 2022.11.19 |