1. 텍스트를 숫자로 바꾸는 작업
- 단어에 번호를 매기고 번호에 해당하는 요소만 1 ,나머지는 0

- N개의 단어가 있다면 각 단어는 한 개의 요소만 1인 N차원의 벡터로 표현 ( 벡터 포현에 어떤 단어 끼리 유사하고, 반대인지 단어와 단어 관계가 전혀 드러나지 않음)
- 이 부분을 좀 더 똑똑하게 바꾸려고 예를 들면 왕↔ 여왕을 남↔녀 관게라는 것을 벡터로 알아낼 수 있기 위해 만든 것이 임베딩 모델 (word embedding)
2. Word2Vec
현대적인 자연어 처리 기법들은 대부분 이 임베딩 모델에 기반을 두고 있다. 그렇다면 어떻게 벡터에 단어의 의미를 담을 수 있을까?
- 우리는 어떤 대상이든 대상의 속성들을 표현하고, 그것을 바탕으로 모델 생성
- 예를들어 버섯을 조사해 놓은 데이터가 있다면 이것은 버섯이라는 ‘대상’을 색깔, 크기 같은 ‘속성’들로 표현한 것이고, 이 정보를 바탕으로 그 버섯이 독버섯인지 아닌지 판별하는 모델 생성 가능
- 이렇게 대상의 속성을 표현하는 방식을 feature representation으로 부름 , 자연어 처리의 경우 대상은 텍스트이고, 이 텍스트의 속성을 표현해놓은 것이 데이터
- 단어에는 어떤 속성이 있을까? 일단 단어 그 자체가 있다. 예를 들어 해당 단어가 ‘강아지’라면 그 단어가 ‘강아지’라는 것 자체가 이 대상의 속성이 됨
- 단어의 품사 , 앞 뒤의 단어, 몇 번째 단어인지 등이 중요한 속성
- 이런 속성들을 어떻게 표현할까? 언어의 속성을 표현하는 방법으로 크게 sparse representation과 dense representation이라는 두가지 방식
- Sparse representation → onehot 인코딩 , dense representation은 임베딩 벡터모델 (word2vec) 을 뜻함
3. Sparse representation
- Sparse representation, 즉 one-hot encoding은 해당 속성이 가질 수 있는 모든 경우의 수를 각각의 독립적인 차원으로 표현
- 해당 단어가 ‘강아지’라는 속성을 표현하려 할 때 우리가 가진 단어가 총 N개라면 이 속성이 가질 수 있는 경우의 수는 총 N개
- One-hot encoding에서는 이 속성을 표현하기 위해 N차원의 벡터를 만듦
- 그리고 ‘강아지’에 해당하는 요소만 1이고 나머지는 모두 0으로 둔다. 이런 식으로 단어가 가질 수 있는 N개의 모든 경우의 수를 표현 가능
- 마찬가지 방식으로 품사가 ‘명사’라는 속성을 표현하고 싶다면 품사의 개수 만큼의 차원을 갖는 벡터를 만들고, ‘명사’에 해당하는 요소만 1로 두고 나머지는 모두 0으로 둔다.

- 벡터나 행렬이 sparse하다는 것은 벡터나 행렬의 값 중 대부분이 0이고 몇몇 개만 값을 갖고 있다는 것을 뜻함
4. Dense representation
- 각각의 속성을 독립적인 차원으로 나타내지 않고 대신 우리가 정한 개수의 차원으로 대상을 대응시켜서 표현
- 예컨대 해당 속성을 5차원으로 표현할 것이라고 정하면 그 속성을 5차원 벡터에 대응시키는 형태로 이대응을 임베딩(embedding)이라 하며 임베딩 방식은 머신러닝을 통해 학습
-
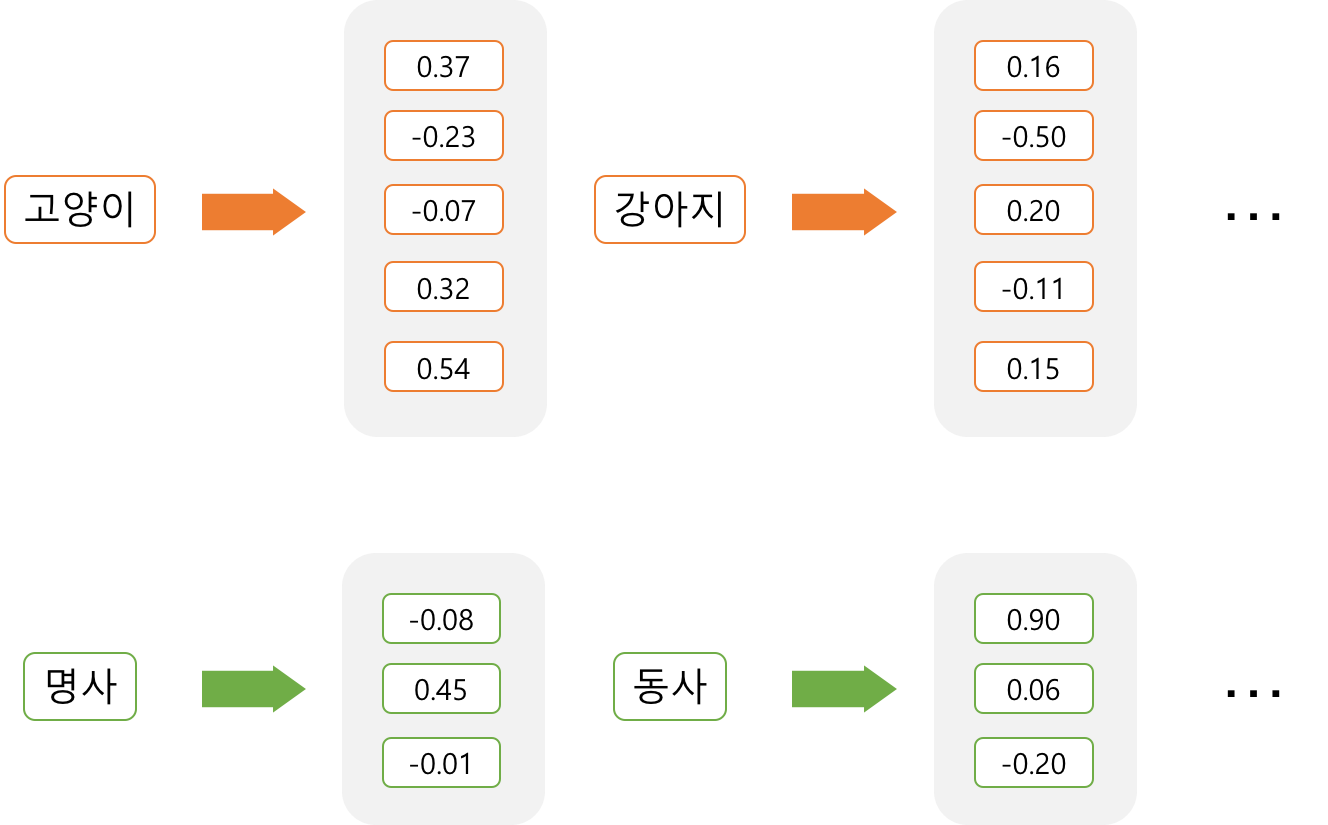
- 임베딩된 벡터는 더이상 sparse하지 않다. One-hot encoding처럼 대부분이 0인 벡터가 아니라, 모든 차원이 값을 갖고 있는 벡터로 표현이 된다. 그래서 sparse의 반대말인 dense를 써서 dense representation 표현이라고 부른다.
- Dense representation은 또다른 말로 distributed representation이라고도 불리는데 ‘Distributed’라는 말이 붙는 이유는 하나의 정보가 여러 차원에 분산 된다는 표현
- Sparse representation에서는 각각의 차원이 각각의 독립적인 정보를 갖고 있지만, Dense representation에서는 하나의 차원이 여러 속성들이 버무려진 정보를 들고 있다
- 하나의 차원이 하나의 속성을 명시적으로 표현하는 것이 아니라 여러 차원들이 조합되어 나타내고자 하는 속성들을 표현
- ‘강아지’란 단어는 [0.16, -0.50, 0.20. -0.11, 0.15]라는 5차원 벡터로 표현
- 다만 ‘강아지’를 표현하는 벡터가 ‘멍멍이’를 표현하는 벡터와 얼마나 비슷한지, 또는 ‘의자’를 표현하는 벡터와는 얼마나 다른지는 벡터 간의 거리를 통해 알 수 있음
- 단어 벡터의 값들은 머신 러닝을 통해 학습된다. 뒤에 나올 word2vec은 이 값들을 학습하는 방법론 중의 하나
5. 수학적으로 이해하기
- CBOW, 즉 문맥에서 한 단어만 보고 타겟 단어를 예측하는 문제 case
- 입력으로 타겟 단어의 앞 단어가 들어가고 출력으로 타겟 단어가 나와야 하는 문제
- V는 사전의 크기(vocabulary size), N은 히든 레이어의 크기(hidden layer size)을 뜻한다.
- 사전의 크기란 다른 말로 단어의 개수, 히든 레이어의 크기는 우리가 단어를 몇 차원으로 임베딩할지를 나타낸다.
-
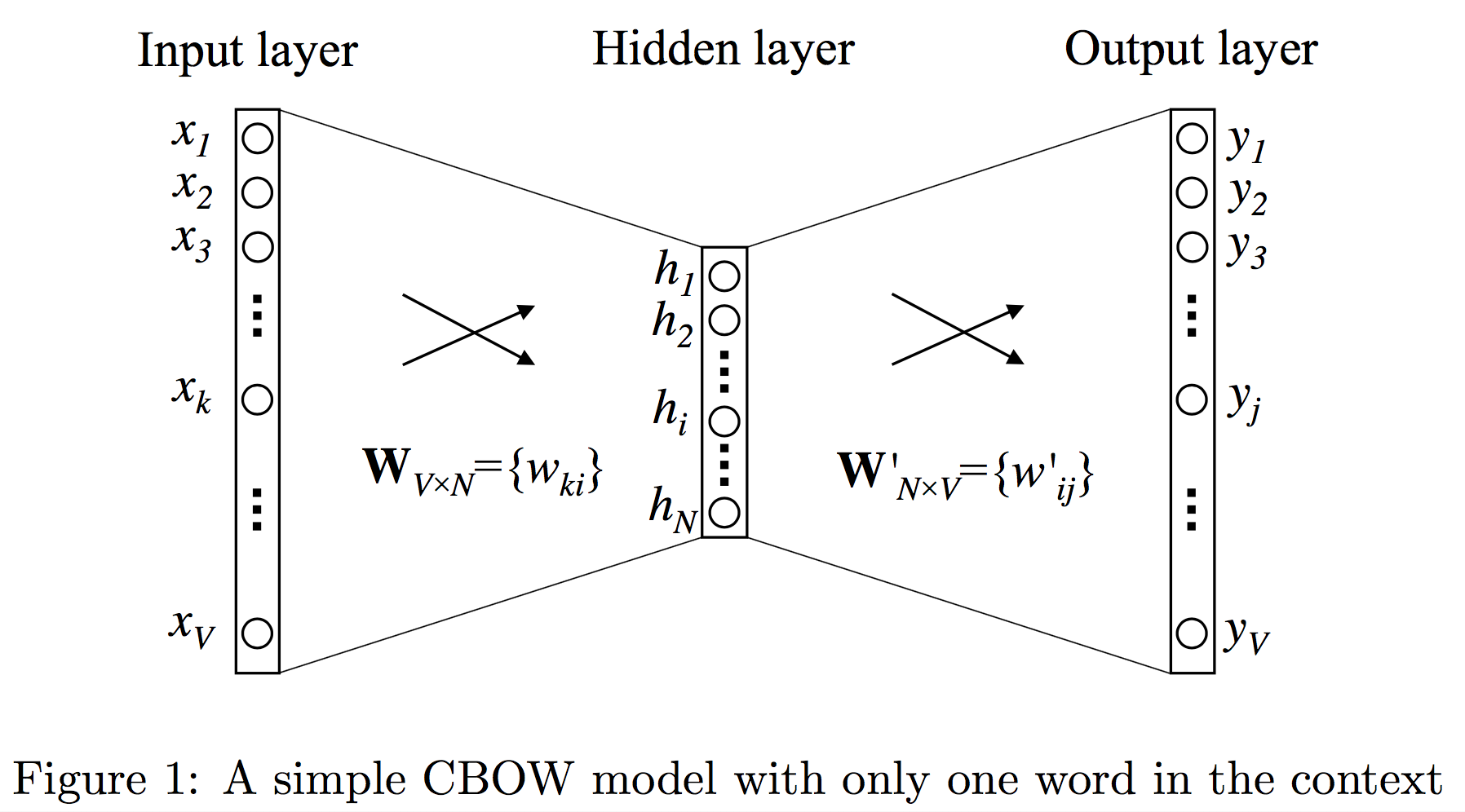
- 입력은 one-hot encoding된 벡터 ,입력 단어, 즉 타겟 단어의 앞 단어는 V개의 요소 중 하나만 1이고 나머지는 모두 0인 벡터로 표현
- 단어의 개수만큼의 차원을 갖는 입력 레이어(input layer)가 히든 레이어(hidden layer)에서 임베딩 크기만큼의 차원의 벡터로 대응된다.
- 출력 레이어(output layer)는 다시 단어의 개수만큼의 차원을 갖는다 , 출력은 타겟 단어이므로 단어의 개수만큼의 경우의 수가 있기 때문이다.
- 입력 레이어(input layer)와 히든 레이어(hidden layer) 사이를 연결하는 파라미터들은 V X N의 행렬 W로 나타낼 수 있고
- 입력 레이어에서 히든 레이어로 넘어가는 것은 단순히 행렬 W를 곱하는 것과 같다
- x가 입력 벡터라고 하면, 히든 레이어 h는 WTx 로 계산된다. 이 벡터는 V차원, 즉 임베딩 차원의 벡터가 된다.
- 입력 벡터 x는 one-hot encoding된 벡터이다. x의 요소 중 k번째 요소만 1이라고 하자. x의 나머지 요소가 모두 0이기 때문에 다른 부분은 모두 무시되고 WTx 의 결과는 WT 의 k번째 열, 즉 W의 k번째 행만 남는다.
- 이 벡터가 해당 단어의 N차원 벡터 표현이 된다. W의 각 행들은 각각 해당하는 단어의 N차원의 벡터 표현인 것
- W의 i번째 행을 vwIT 라고 부르면, 히든 레이어 h는 vwIT와 결국 같다는 것을 알 수 있다.

- 입력 레이어에서 히든 레이어로 넘어가면서 우리는 히든 레이어 h를 얻었다. 히든 레이어에서 출력 레이어로 넘어가기 위해, 우리는 또다른 행렬 W′ 가 필요하다. W′ 는 N X V의 행렬
- 이 파라미터 행렬을 이용해서, 우리는 모든 단어에 대해 출력 레이어의 점수 uj를 계산할 수 있다. 아래 식에서 zwj는 W′의 j번쩨 열을 뜻한다. 즉 uj 는 j번째 단어에 대한 예측 점수
- 입력 레이어에서 히든 레이어로 넘어가면서 우리는 히든 레이어 h를 얻었다. 히든 레이어에서 출력 레이어로 넘어가기 위해, 우리는 또다른 행렬 W′ 가 필요하다. W′ 는 N X V의 행렬이다
- 이 파라미터 행렬을 이용해서, 우리는 모든 단어에 대해 출력 레이어의 점수 uj를 계산할 수 있다. 아래 식에서 zwj는 W′의 j번쩨 열을 뜻한다. 즉 uj 는 j번째 단어에 대한 예측 점수이다.
- 예측 점수를 각 단어의 확률값으로 바꿔주기 위해 softmax를 쓴다. 이는 각 단어의 점수에 비례하여 점수를 확률로 만들어주는 방법이다. 이 방식을 통해 각 단어의 예측 점수가 모두 0 이상이고 모두 더하면 1이 되는 확률값으로 변한다.
- 여기에서 yj 는 출력 레이어의 j번째 출력값이다. 위 식들을 조합하면 최종적으로 아래와 같은 식을 얻는다.


- 결과적으로 단어 w는 두가지 벡터로 표현된다. 바로 vw 와 zw 이다. zw는 입력 레이어에서 히든 레이어로 넘어가는 행렬 W에서 나오며, zw는 히든 레이어에서 출력 레이어로 넘어가는 행렬 W′ 에서 나온다
- vw를 단어 w의 입력 벡터(input vector), zw를 단어 w의 출력 벡터(output vector)라고도 부른다.
- W에 input을 곱해 나온 h 상태의 벡터 → h 는 임베딩 된 단어 , W, W` 중 하나만 쓰거나 둘을 평균내서 임베딩 벡터로 사용
- word2vec에서 학습은 의미가 비슷한 단어들 간의 거리를 좁히고 서로 의미가 다른 단어들 간의 거리를 멀게 하는 역할
- 주변단어로 중심단어를 예측하는 문제를 풀다보면 주변단어가 비슷하면 비슷한 벡터로 매핑되고 주변단어가 다르면 다른 벡터로 매핑
- 좋은 임베딩은 비슷한 단어에 대한 벡터 사이 거리가 작은 임베딩 ( 트레이닝이 되는 원리는 backpropagation, 즉 결국 미분한 뒤 극소값을 찾아가는 과정)
- input vector와 output vector를 조합하는 방법은 두개를 더하거나, 평균 내는 등의 방법
반응형
'Deep Learning' 카테고리의 다른 글
| 손실함수 , 활성함수 정리 (0) | 2023.09.06 |
|---|---|
| Embedding layer와 Embedding Vector의 Output 차이 정리 (0) | 2023.02.14 |
| Dynamic programming (0) | 2022.05.15 |
| Markov Reward Process (0) | 2022.05.15 |
| 강화학습 (Reinforcement Learning) (0) | 2022.05.13 |