일반 선형 확률 과정(General Linear Process)
일반 선형 확률 과정이란 시계열 데이터가 가우시안 백색잡음의 현재값과 과거값의 선형조합
- 가우시안 노이즈 : 정규분포를 갖는 잡음, 일반적인 잡음으로 갑자기 튀는 잡음이 아님
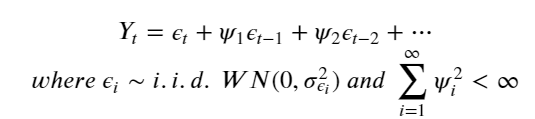
- e_t : 잡음의 현재값, e_t-1 : 잡음의 과거 값 , w : 특정한 비율
결국 잡음의 현재값과 과거값에 특정비율을 곱한 것들의 합, 변수는 서로 독립이며 정규분포 기준으로 평균이 0이고분산이 특정한 범위에 있음, weight값의 제곱의 합이 무한대 보다 작다 -> 제곱합을 무한대로 더해서 무한대보다 작으려면1보다 작아야함(1미만을 제곱해서 무한대로 더하면 무한대보다 작기 때문)결국 어떠한 타임포인트 던지 다 쪼개서 작은 값으로 백색잡음에 비율(웨이트)을 곱한 것으로 표현하면 어떠한 값도 표현할 수 있다는 것이 시계열의 전통적인 알고리즘의 방향
-> 결국 더하기로 (선형조합)으로 구성되어 있음
일반 선형 확률 세부 알고리즘
ex) WN,MA,AR,ARMA,ARIMA,SARIMA
1) White noise
1) 잔차들은 정규분포이고, (unbiased) 평균 0과 일정한 분산을 가져야 하고 ,Covariance = 0
2) 잔차들이 시간의 흐름에 따라 상관성이 없어야 함
특성요약:
- 강정상 과정(Stictly Stationary Process)
- 강정상 예시로 시계열분석 기본알고리즘 중 가장 중요함
- 시차(lag)가 0일 경우, 자기공분산은 확률 분포의 분산이 되고 시차가 0이 아닌 경우, 자기공분산은 0.
- 시차(lag)가 0일 경우, 자기상관계수는 1이 되고 시차가 0이 아닌 경우, 자기상관계수는 0.
- 𝜌𝑖={10 for 𝑖=0 for 𝑖≠0
2) Moving Average
- 𝑀𝐴(𝑞) : 알고리즘의 차수(𝑞)가 유한한 가우시안 백색잡음과정의 선형조합
- EXponential Smoothing 내 Moving Average Smoothing은 과거의 Trend-Cycle을 추정하기 위함이고, MA는 미래 값을 예측하기 위함
- MA 알고리즘은 어떤 ACF플롯이 나오는 지를 봐야함 -> 이를 알아야 어떤 알고리즘의 특성이 있는지 체크하기 위함
- * ACF : t개의 값을 가지는 독립변수 X와 이에 대응하는 종속변수 Y 간의 상관관계를 정량적으로 찾는 알고리즘인 회귀에서 잔차들이 시간의 흐름 따라 독립적인지를 확인하기 위해서 실행하는 자기 상관분석
- 현재의 Y값과 과거의 Y값의 상관성을 비교
- X: y의 LAG , y: correlation 으로 아래와 같은 그래프의 형상은 정상적 ( 시간에 따라 y가 독립적이기에)
- Correlation = Covariance + varience +E

MA(1):

MA(2):

3) AR(Auto -Regressive)
AR(p) : 알고리즘 차수(p)가 유한한 자기자신의 과거값들의 선형 조합
- 필요성 : ACF가 시차(Lag)가 증가해도 0이 되지 않고 오랜시간 남아있는 경우에 MA모형을 사용하면 차수가 무한대로 감
MA (무한대) 모델과 = AR(1)
MA랑(ACF)은 다르게 AR모형에서는 PACF로 파라미터 수를 판단할 수 있음


4) Relation of MA and AR
- 가역성 조건(Invertibility Condition):
1) 𝑀𝐴(𝑞) -> 𝐴𝑅(∞): 변환 후 AR 모형이 Stationary Condition이면 "Invertibility"
2) 𝐴𝑅(𝑝)-> 𝑀𝐴(∞) 여러개 모형변환 가능하지만 "Invertibility" 조건을 만족하는 MA 모형은 단 1개만 존재
5) ARMA( Auto -Regressive Moving Average )
"𝐴𝑅𝑀𝐴(𝑝,𝑞): 알고리즘의 차수(𝑝 𝑎𝑛𝑑 𝑞)가 유한한 𝐴𝑅(𝑝)와 𝑀𝐴(𝑞) 의 선형조합 (AR + MA)
AR과 MA의 정상성 조건과 가역성 조건이 동일하게 ARMA 알고리즘들에 적용
종속 변수 Y_t는 종속변수 Y_t와 백색잡음(et) 차분들(Lagged Variables)의 합으로 예측 가능
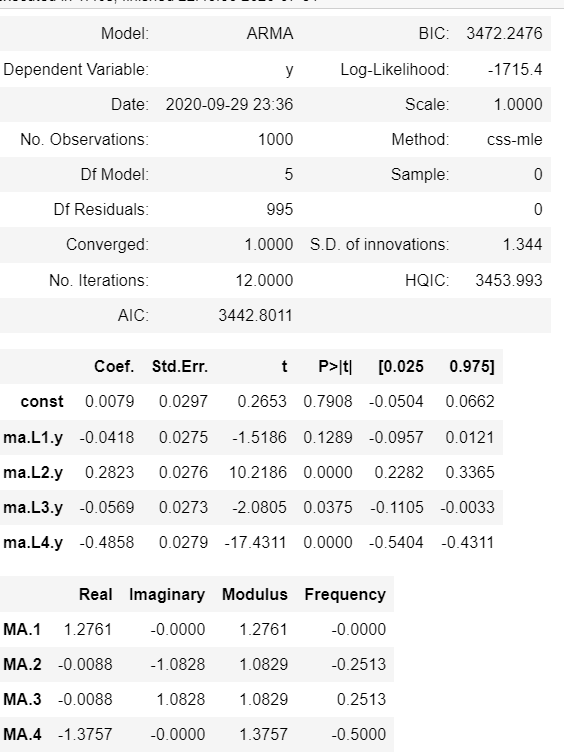
파라미터의 수가 늘어나면 유효하지 않은 t>0.05 변수들이 생겨남 ( 변수가 적을 때 유효했더라도)
AR과 MA를 같이 사용하기 시작하면 ACF,PACF가 예상과 다르게 나올 수 있기에 이것으로는 판단하기 어려움
-> 통계량으로 적절한 변수 사용
Log Likelihood , AIC,BIC 가 낮아지면 낮아질 수록 잘 피팅 된 것
6) ARIMA( Auto -Regressive Integrated Moving Average )
차분이 적용된 AR(p)과 MA(q)의 선형 조합 -> 차분(Trend,Seasonal) 을 통해 비정상 시계열을 정상 시계열로 만들고 ARMA를 적용하는 모델
- 비정상성인 시계열 데이터 𝑌𝑡를 차분한 결과로 만들어진 데이터이고 ARMA 모형을 따르면 원래의 𝑌𝑡를 ARIMA 모형이라고 함
- 𝑑번 차분한 후 시계열 Δ𝑑𝑌𝑡Δ가 정상성인 데이터이고 ARMA(p,q) 모형을 따른다면 적분차수(Order of Integrarion)가 𝑑인 ARIMA(p,d,q)로 표기함
- 𝑝=0: ARIMA(0,d,q) = IMA(d,q)
- 𝑞=0: ARIMA(p,d,0) = ARI(p,d)
ARIMA (0,0,0) : WHITE NOISE
ARIMA (0,1,0) : RANDOM WALK -> 수식으로 증명 가능
하나하나 설명이 어려우니 아리마로 모든 것을 설명함
'Time Series Model' 카테고리의 다른 글
| 상태 공간 모형 기반의 로컬 레벨 모형 및 시계열 구조화 모형 (0) | 2023.05.22 |
|---|---|
| 상태 공간 모형 기반의 지수 평활법 및 선형 추세 알고리즘 (0) | 2023.05.17 |
| 시계열 데이터 - (one step ahead cross validation) (0) | 2021.07.16 |
| 시계열 분석 (Time Series) (0) | 2021.07.16 |