* 협업 필터링 (Collaborative Filtering)
협업 필터링은 어떤 특정한 인물 A가 한가지 이슈에 관해서 인물 B와 같은 의견을 갖는다면 다른 이슈에 대해서도 비슷한 의견을 가질 확률이 높을 것
Memory-based 협업 필터링의 추천 시스템은 유사도를 기반으로 동작
Movie Lense Dataset
1. ratings.dat
2. movies.dat -> 위의 두가지의 데이터셋을 통해 Rating Matrix를 만드는 것이 목표
Object : 특정 시간 이전에 시청했던 영화들을 통해 앞으로 어떤 영화를 볼 지 예측하는 것

user = 7명 (u)
영화 = 5개 (i)
7*5=35개의 총 평가지표(유저 x 아이템)
->1번 유저가 보지않은 2번과 5번 등 아직 빈칸이 있는 곳을 예측 하는 것이 rating matrix (가장 기본적인 추천시스템)
* rating matrix 의 대표적인 두가지 예시가 CF ,MF
* Colaborative Filtering (CF)

미영에게 어떤 영화를 보여줘야 가장 잘 추천한 걸까?
미영의 {레디플레이원,곤지암}을 가장 비슷하게 평가한 사람이 철수
-> 그렇다면 미영도 인피니트워를 재미있게 볼 것이다 라는 것이 CF
이렇게 비슷한 유저를 찾아서 아이템을 추천해주는 것 = user based
열을(item) 기준으로 사람을 추천 하는 것 = Item based
단 item based 는 사전 데이터가 없으면 추천이 불가 (cold start)
* suprise의 KNN - CF의 가장 기초가 되는 알고리즘
[KNN의 대략적인 이해] 1.
새로운(혹은 특정한) 데이터 포인트 X가 있을 때, X와 가장 유사한 k개를 이용하여 데이터 포인트 X의 위치를 찾는 알고리즘
2. euclidean distance, cosine similarity 등을 기준으로 유사한 k개를 계산
3. 분류(classification) 문제의 경우는 k개의 포인트에서 가장 많이 등장한 class로 할당
4. 예측(regression) 문제의 경우는 k개 포인트의 평균 값, 혹은 가중치 값 등으로 X의 값을 예측
-> 추천의 관점에서는 철수와 영희가 얼마나 가까운지를 보여주는 모델


[라이브러리의 대략적인 학습 과정]
1. User-based CF
2. 유저 A와 가장 영화를 유사하게 평가한 유저 k명을 선정
3. k명의 유저가 영화 a를 평가한 점수를 활용하여 위의 식대로 점수를 계산함
-> k개의 평균값을 예측 점수로 나타내는 것
4. 이와 같은 방식으로 Rating Matrix를 완성
STEP 3 . MF-Based 모델링 (SVD)


CF based -> 가장 비슷한 열이나 행을 찾아서 가장 비슷한 N개의 평균을 낸다거나 다른 지표로
어떤 다른 인사이트를 찾는 것 -> 사람의 추론과정과 비슷
but , MF -> 매트릭스의 빈공간을 수학적(행렬분해)으로 완성시키는것 R=P *Q^t
[MF의 대략적인 이해]
1. 원래의 행렬을 다른 2개 행렬로 분해하고, 이를 다시 원래 모양으로 만드는 과정을 Factorization 이라고 함.
2. 그 과정에서 Latent Factor 라는 것을 활용하여, 행과 열의 성질을 만들어낼 수 있음.
3. latent factor를 충분히 많이 만들게 되면, 유저와 아이템의 성질을 벡터로 표현 가능.
4. 일반적으로 지도 학습을 통해 P와 Q를 찾게 되고, 이를 Model-based CF 라고 하기도 함

결국 R 값이 -> Rate로서 Regression으로 표현 가능
* MF 모델링 결과

-> 파라미터 튜닝


최적의 파라미터는 = 50
결국 MF가 CF보다 이번 실험에서는 기술적으로 높다
-> but 유저 기준으로 평가할 때
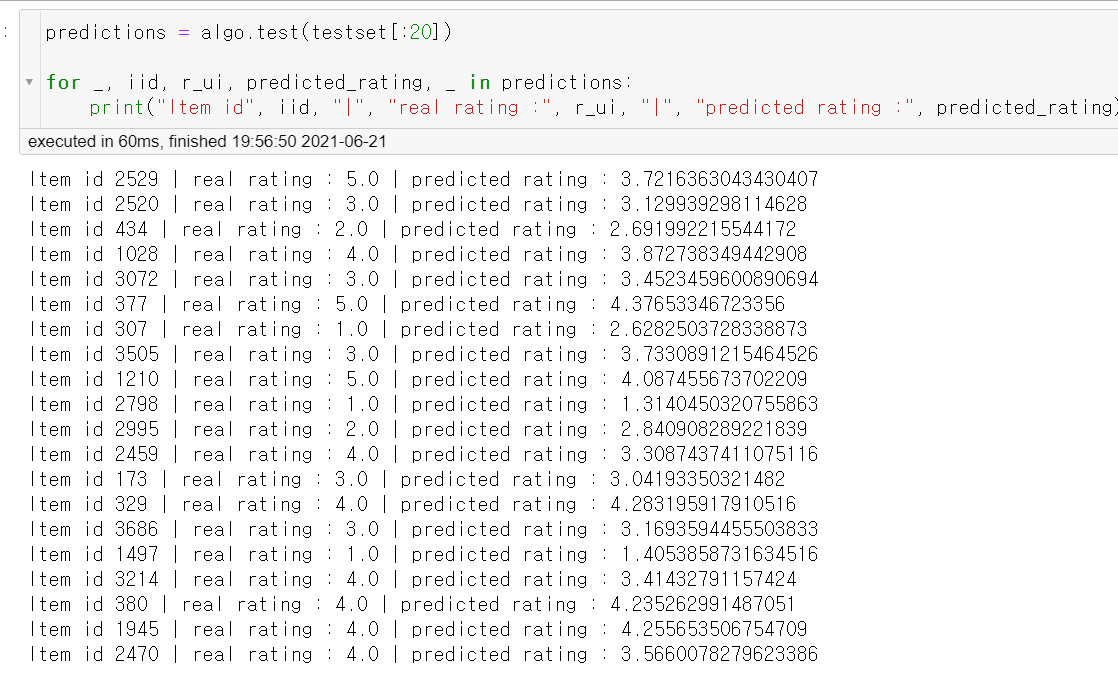
* id 2529 의 실제 점수는 5.0 예상점수는 3.72
Step 4. 추천 결과 평가
CF, MF 기반 추천시스템의 가정(한계)[가정 : 사용자의 과거 Preference는 미래에서도 동일하다]
1. Time Series로 추정된 선호도가 아닌, Estimate 되거나 Factorized 된 점수
2. A시점에 평가한 선호도와, B시점에 평가한 선호도가 동일 선에서 학습됨
3. Test 데이터에 대한 평가 역시, 시간이 고려되지 않은 "랜덤한 빈공간 찾기" 식으로 평가됨
-> 메트릭스의 빈칸을 예측하는 것이 무조건적인 object가 된다면 정확한 output을 낼 수 없다
- 이번 Research의 목표
- RMSE가 낮더라도 추천시스템을 정확하게 평가할 수 있는 시계열 적인 factor를 고려하자

[Confusion Matrix와 Recall]
1. 분류 문제에서 사용하는 대표적인 평가 기준
2. 무언가의 실제 클래스(binary), 그리고 예상한 클래스(binary)를 비교하기 위한 매트릭스
3. 이 중 Precision은 흔히 "정확도" 이라고 불리는 지표로, 맞다고 예측한 것 중에 실제로 맞는 것의 비율을 의미함.
[추천시스템과 Precision, Recall]
1. 추천시스템에 이를 대입해보자
2. 유저A가 실제로 시청한 영화들을 a, 모델이 유저 A가 볼 것이라고 예측한 영화들을 b라고 가정
3. 이 때 모델이 10개의 영화를 예측 했다면 Top 10 Precision 계산할 수 있음.
4. Recall 역시 마찬가지의 방법으로 구할 수 있음.
5. Precision과 Recall에 대한 선택 기준은 상황마다 다르지만, 추천시스템에서 일반적으로 사용하는 지표는 "MAP"
6. MAP(Mean Average Precision) : 추천시스템에서는 각 유저마다의 Precision을 계산한 뒤, 이것을 모든 추천 대상 유저로 확장하여 평균적인 지표를 계산한 것이라고 볼 수 있음.
'Recomendation System' 카테고리의 다른 글
| Matrix Factorization 적용 - SGD , ALS (0) | 2023.03.07 |
|---|---|
| Latent Factor model (0) | 2023.03.07 |
| Association Rules + FP Growth (0) | 2023.03.07 |
| 추천 시스템 설계 구성안 (Tmall) (0) | 2022.09.22 |