Factorization Machine 논문 리뷰

Abstract

• Factorization machine은 SVM과 Factorization Model의 장점을 합친 모델
  • FM 예시 : Matrix Factorization, Parallel factor analysis, specialized model(SVD ++, PITF or FPMC)
  • SVM : 큰 데이터에서 support vector를 찾아서 support vector를 기준으로 데이터를 classification/regression 
    • 일반적으로 머신러닝에서 자주 쓰이는 알고리즘
• Real valued Feature Vector를 활용한 General Predictor
  • FM은 classification/regression 등 다양한 문제들을 general하게 풀 수있는 모델
• Factorization Machine의 식은 linear time
  • linear하다 -> 계산 복잡도가 크게 복잡하지 않다 -> 비교적 간단하게 풀 수 있는 것이 장점
• 일반적인 추천시스템은 special input data, optimiztion algorithm 등이 필요
• 반면, Factorization Machine은 어느 곳에서든 쉽게 적용 가능
  • FM 개념 자체가 Special 한 input 이 필요하지 않고 어느  황에서나 적용 가능한 좋은 모델

 

Introduction

• Factorization Machinedms general predictor로, high sparsity에서 reliable parameter를 예측 가능
• sparse한 상황에서 SVM은 부적절함
  • cannot learn reliable parameteres(hyperplanes) in complex(non-linear) kernel spaces
  • svm은 feature engineering 상황에서 null 값이 없는 DF를 만들어서 학습하는 것에 익숙함 
    • but FM은 해당 sparse한 상황에서도 학습을 하여 general predict가 가능
• FM은 복잡한 interaction도 모델링하고, factorized parametrization을 사용함
• Linear Complexity이며,linear number of parameters 임
  • 성능도 좋은데 속도도 빠르다는 의미

 

Contributions

• Factorization Machine은 다음과 같은 장점이 있다.
• Sparse data(일반적인 상황) , Linear Complexity, General Predictor로서 추천 이외에 다른 ML에서 사용 가능함

 

• 일반적으로 볼 수 있는 영화 평점 데이터의 설명 (위의 data S처럼 obeserved data set을 만들 수 있음)
• Factorization Machine은 user,movie,rating 뿐 아니라 더 다양한 feature 들을 사용 가능
  • Matrix Factorization은 user와 movie, 그리고 해당 rating만 사용

 

Prediction Under Sparsity

 

• MF 같은 경우는 user와 movie의 행렬을 가지고 학습을 함
• FM은 user, movie(어떤 영화를 봤는지), user가 평가한 다른 item(implict data), time ,직전 평가한 item 등 여러 feature들을 포함하여 학습함(one- hot 형태로 표현) 
  • FM은 feature를 구성할 때 support vector machine과 비슷한 특징을 가지고 있음

 

 

FM - Model Equation (1)

 

 

• x_i는 feature vector, x_i에 맞는 w를 학습하는 것
• v_i,v_j는 Size k의 두 벡터를 내적하는 부분(MF 개념을 가져옴) -> 이 부분으로 인해 linear하게 계산 됨
• 2- way FM(degree = 2) : 개별 변수 또는 변수간 interaction 모두 모델링 진행
  • degree가 2이상이어도 상관 없음
• 다항 회귀와 매우 흡사하지만,coefficient 대신 파라미터마다 embedding vector를 만들어서 내적함

 

FM - Model Equation (2)

빨강 상자 식

• Matrix Factorization -> W_u * W_i 
  • user와 item latent vector ( user와 item의 interaction 만 고려할 수 있음)
• Factorization Machine -> W_i * x_i
  • x_i (feature vector) 마다 구한다  ( feature , item, user 등의 모든 interaction을 고려 할 수 있음)

파랑 상자 식

• 변수간 latent vecotr 조합을 고려함
• degree = 2 인 경우 모든 interaction을 얻을 수 있음
• pairwise feature interaction을 고려하기 때문에 sparse 한 환경에 적합하다

 

 

Factorization Machine as Predictors

• general predictor 로서의 역할
  • 1. Regression -> y^을 regression으로 풀 수 있음 (least square error)
  • 2. binary classification -> y^을 0또는 1을 지정하여 풀 수 있음
  • 3. Ranking -> pairwise classifcication loss를 사용해서 score of y^을 점수로 sorting하여 ranking화 가능
• 위와 같은 케이스에서 결국 L2와 같은 regularization term을 넣어서 overfitting을 방지할 수 있음

 

Learning Factorization Machone

• 빨강 상자가 gradient인데 해당 gradient를 업데이트 하면서 FM을 학습하는 방식
  • stochastic gradient descent

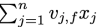
• 위의 수식이 i에 독립적이라 미리 계산을 할 수 있어 그렇기에 constant time에 계산 될수 있음
  • time complexity가 떨어진다는 의미
• 모든 파라미터 업데이트는 sparsity한 상황에서도 time complexity가 O(K n)

 

 

d-way Factorization Machine

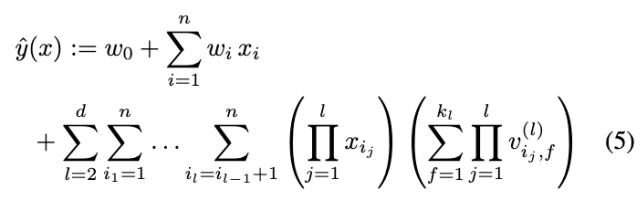
• y^이라는 식을 2way로 위에는 살펴봤는데 2이상으로도 일반화를 할 수 있음
• 마찬가지로 computation cost는 linear함
• 다양하게 활용할 수 있는 모듈 공개 (http://www.libfm.org)

 

Additional Experiments

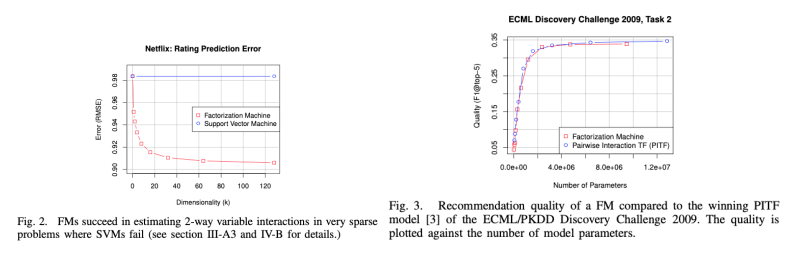
• FM의 general predictor로서의 역할(분류,회귀,랭킹)등에 대한 적용 예시(비교적 좋은 성능)
  • ECML challenge에서 sota 모델(PITF)과 fm이 동급 성능을 나타내는 것을 보여줌
  • 그러나 FM은 PITF는 다르게 랭킹 뿐아니라 회귀 분류등 여러개의 태스크에서 사용 가능

Conclusion

• Factorized Interaction을 사용하여 feature vector x의 모든 가능한 interaction을 모델링 함
• High sparse한 상황에서도  interaction 추정 가능, unobserved interaction에 대해서도 일반화 가능
• 파라미터 수, 학습과 예측 시간 모두 linear함 (Linear complexity)
• 이는 SGD를 활용한 최적화를 진행할 수 있고 다양한 loss function을 사용할 수 있음
• SVM, matrix, tensor and specialized factorization model 보다 더 나은 성능을 증명함

 

 

---

참고 :  

1)  https://ieeexplore.ieee.org/document/5694074 (Factorization Machine 논문)